7. The Quadralectic Theory

The theoretical background of the quadralectic way of thinking is given here only for those readers with an interest in these matters. There is a distinct difference between the philosophical approach to division thinking and the mathematical appreciation of its foundations. The former is part of a wider field of human knowledge and is highly influenced by subjective notions, which are part of the development of thought within the context of cultural achievement. The latter is a formalized method, which is bound by its own logic and has a more objective nature. Mathematics concerns itself with the development of a universal language to communicate in terms of given standards.

The quadralectic theory is the adaptation, or better: formalization, of the modern four-fold way of thinking within the language of mathematics.  Empedocles’ efforts – to name fire, air, earth and water as the basic elements of nature – were a proposal to understand the visible world in tetradic terms. The Scholastic theory of the four senses – as a method to understand the meaning of a given text (anagoge, allegoria, historia and tropologia) – is the formal predecessor of the quadralectic way of thinking, because it brought order into the different forms of (Bible) interpretation (exegesis).

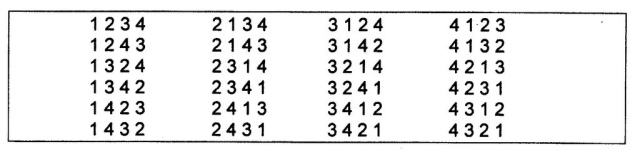
Any mathematical evaluation of the four-division has to take a more ‘neutral’ stand towards the subjective interpretation given to the various elements of the four-division. Every part of the four-division – called a quadrant – is regarded as an individual entity, with no direct relation to the valuation of other quadrants. Therefore, the main aim in the mathematical approach is the elimination of the importance of the order of ranking. The arithmetical sequence 1 2 3 4 is just one way in which the combination of figures (as representation of the quadrants) can be written.

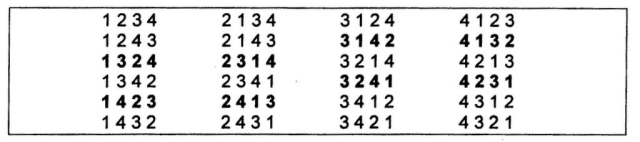
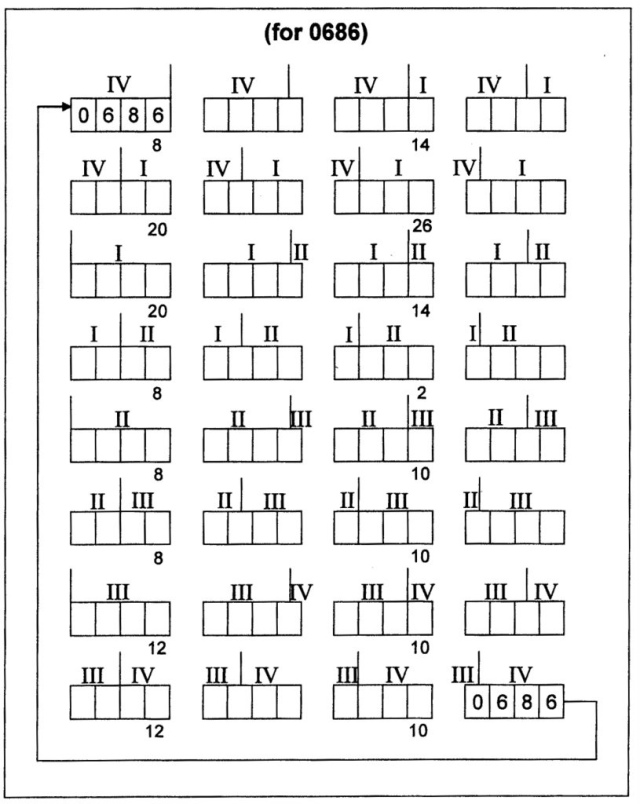
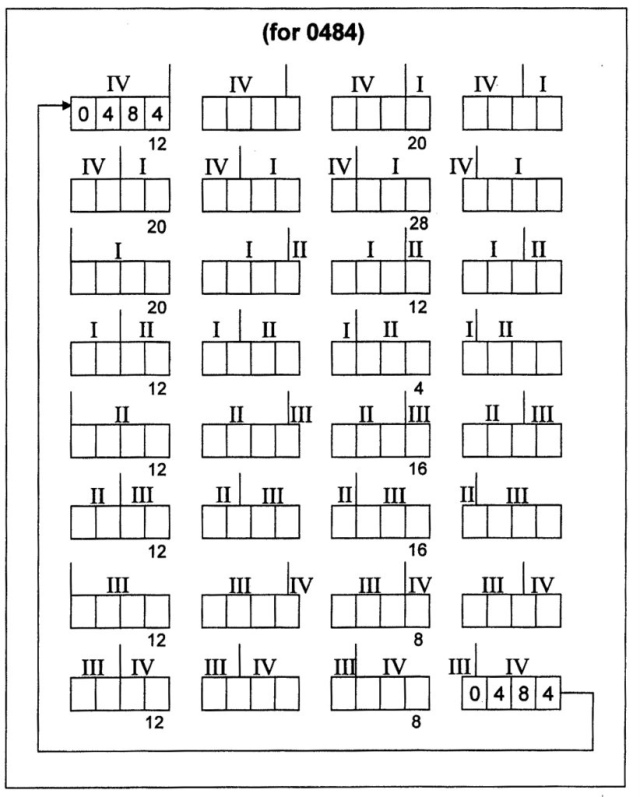
There are twenty-four (24) ways (groupings) in which the sequence 1 2 3 4 can be written (fig. 826):

 Fig. 826 – The numerical sequence 1 2 3 4 can be arranged in twenty-four groupings. The groupings are the prime material for the process of an internal shift, which will unfold the way to an objective valuation.

Every grouping  – which is viewed as a sequence – can be used as a unit of measurement.  At present, the common mathematical sequence is 1 2 3 4, which implies that every second number is ‘higher’ than the previous one.  This is the so-called classical sequence. However, it must be remembered that such a sequence is just a choice. Any of the above-mentioned sequences can be used a base for measurements.

The quadralectic approach takes this arbitrariness into account. It aims at an initial valuation system, which is independent of the order of ranking.  This neutrality can be best achieved in a cyclic environment.  The effect of a cumulative hierarchy is moved to a later stage in the communication.

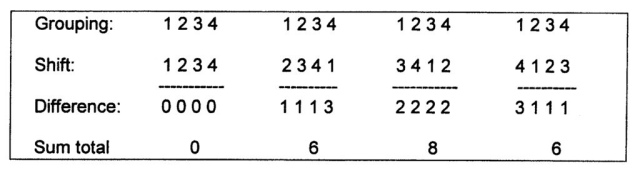
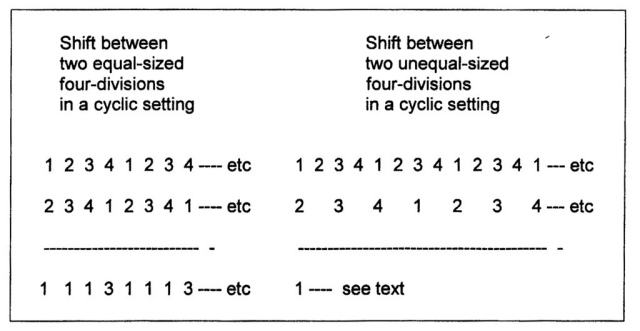
The neutrality of valuation is created by  a shift of the sequence within itself. Separate ranking-orders are joined together in a new valuation unit. The assumption will be that all parts are – internally – of the same size. A cyclic shift of the classical ranking order (1 2 3 4) within itself and to the left will give the following differences (fig. 827):

Fig. 827 – The shift (to the left) of the classical sequence 1 2 3 4 along itself. The sum total is a measure of the commensurability within the shift process and gives a displacement sequence. A movement (shift) of the lower grouping to the right will result in the same sequence (0 6 8 6).

The individual numbers in the displacement sequence  0,  6,  8,  6 are called the communication-coefficient  (CC), indicating the differences of the shift within a given quadralectic unit.

The communication coefficient CC is the sum total of the shift values within a given grouping combination of ranking orders.

The CC is a measure for the internal displacement of the compartments within a division. Zero (0) means no displacement; eight (8) is the maximum displacement. The number is an indication of the commensurability within a given shift. Commensurability is defined here as ‘a common measure between like quantities’ and is seen as a rational number expressing the ratio between quantities (in this case a sequence). This notion will be the backbone of the modern type of quadralectic visibility.

The internal shift within the classical sequence 1 2 3 4 produces a succession of displacement-values, the numbers 0 6 8 6 (fig. 827). This sequence is called the displacement series A.

A displacement series consists of four communication coefficients derived from a complete internal shift within a grouping of ranking orders.

The classical sequence 1 2 3 4 is only one of the twenty-four groupings, which can be obtained within a given four-division, as can be seen fig. 826. Another type of sequence will have influence on the calculation of the displacement values. The other 23 groupings were studied in order to measure their effects on the displacement series. The calculations resulted in only two different rows of displacement values.

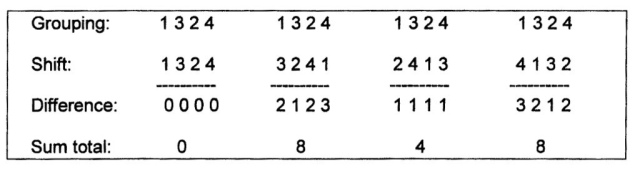
Firstly, as given above, there is the CC-sequence 0 6 8 6 (the A-series), which was applicable for sixteen (16) combinations. Secondly, there were eight (8) other combinations, which gave the CC-sequence 0 8 4 8. This sequence was called the displacement series B. An example of its formation is given below (fig. 828):

Fig. 828 – A shift (to the left) of the sequence 1 3 2 4, which give the sum totals of 0 8 4 8. This row is called the displacement series B. The shift (of the lower unit) to the right will give the same result.

The distribution of the different types (A or B-series) within the total of twenty-four (24) groupings are given below (fig. 829). The classical A-series (based on the CC-sequence 0 6 8 6) consists of sixteen (16) groupings, printed in normal letter type. The B-series (based on the CC-sequence 0 8 4 8) comprises eight (8) groupings, printed in bold:

Fig. 829 – The distribution of the A series and the B-series (bold print) in the twenty-four groupings of the four division.

Both types of sequences have to be taken into account if the displacement series are used in the remaining operation to establish the most neutral ‘counting system’. The purpose of this investigation is to find a measure that can be applied for all shifting four-divisions, regardless of their initial setting and direction.

The displacement series (A and B) are in the foregoing stage observed in a dynamic environment ruled by multiplicity. The next step will lead into an area of restrictions in order to come to a valuation. Only at the very end of the investigation the multiplicity will return again.

The next step will be the valuation within the communication shift. It can be imagined that the participating four-divisions are of unequal length. The movement is in that situation no longer confined to the internal shifting within itself, which is essential the case in the previously given example, but comprises two four-divisions of variable sizes. This situation opens up the confinement of the boundaries of a given (single) part and extends the theory into the interaction of (multiple) parts. The figure below will give an indication of the difference between the procedure (fig. 830).

Fig. 830 – An example of the difference between a shift (within the classical ranking order 1 2 3 4) of equal and unequal-sized four divisions. The boundaries of the shifting four-division play a much more obvious role in the calculation of the communication coefficient (CC) in the case of unequal-sized divisions.

The calculation of the (shift) differences is, in the second case of the unequal-sized four divisions, not as clear-cut as the shift between equal-sized four divisions. An internal shift gives no problems, because the part-itself is the boundary. Unequal parts moving along each other need a limitation of the area of interaction before a (shift) value can be established. A communication trajectory (CT) has to be established in order to limit the field of measurement.

The limitation of the trajectory is established by the width of the Small Part (SP, Minor). This is an important rule that can be stated as follows:

The calculation of the shift-values between two revolving four-divisions, which provides a measure of commensurability in a communication, is limited by the smallest part, which participates in the communication.

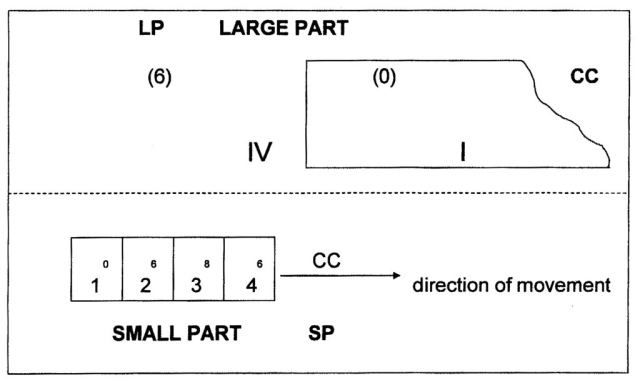
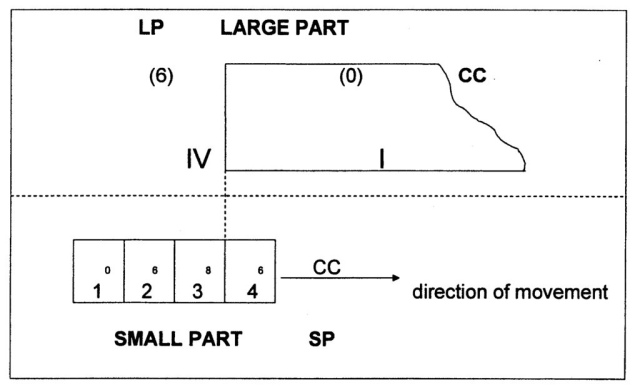
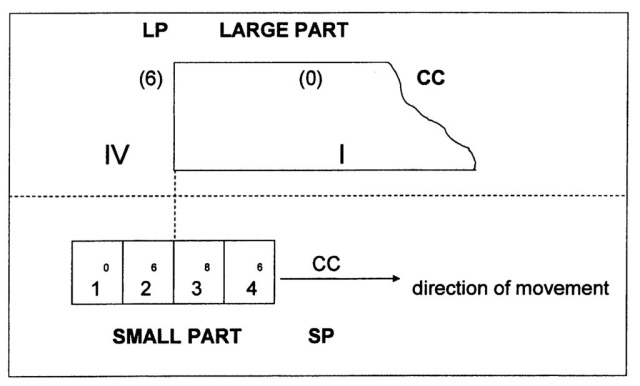
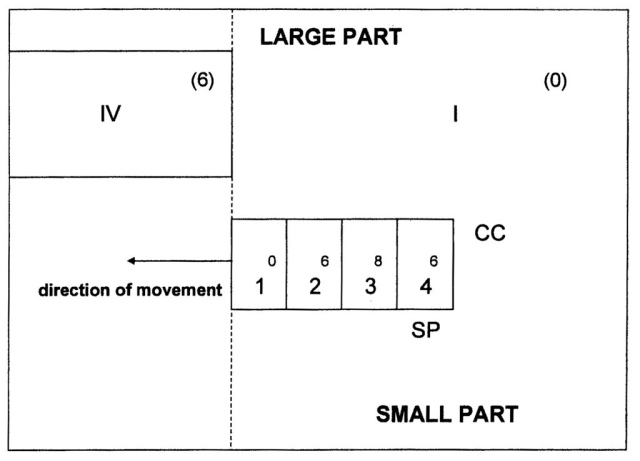
The theoretical process can be clarified in the following way. A (very) Large Part (LP, Major), consisting of the quadrants I, II, III, IV is interacting with a Small Part (SP, Minor), consisting of the quadrants 1, 2, 3, 4.

For the initial valuation (of the shift between the two four-divisions) the A-row of shift-values (0 6 8 6) is proposed. Furthermore, a situation is visualized in which the Minor or Small Part (SP) approaches the Major or Large Part (LP) from the left, i.e. the Fourth Quadrant of Minor (SP) approaches the First Quadrant of Major (LP; see fig. 831). Later the various other possibilities of interaction will be studied.

Fig. 831 – A graphic representation of the approach (from the left) of a  Minor or Small Part (SP) to the First Quadrant of a Major or Large Part (LP). The Small Part is in this (cyclic) setting situated in the Fourth Quadrant of the Large Part.

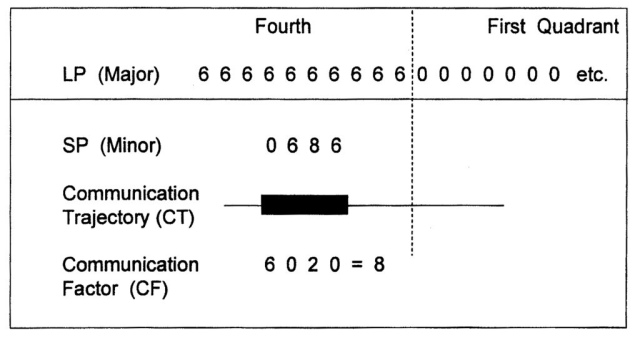
The Minor is placed in an arbitrary position ‘before’ the First Quadrant of the Major (LP). This is, in a cyclic setting, the Fourth Quadrant of a previous cycle of the Major. This ‘space’ is valued with a 6, the last Communication Coefficient (CC) of the A-row: 0 6 8 6. The Small Part (SP) is completely embedded in the last quadrant of the previous cycle of the Large Part (LP), because this quadrant is – by definition – much bigger than the Small Part. The difference in shift-values (CC) is calculated by subtraction.

The sum of the differences, measured over the communication trajectory (CT), provides a number, which is a standard for the shift between two communication partners.

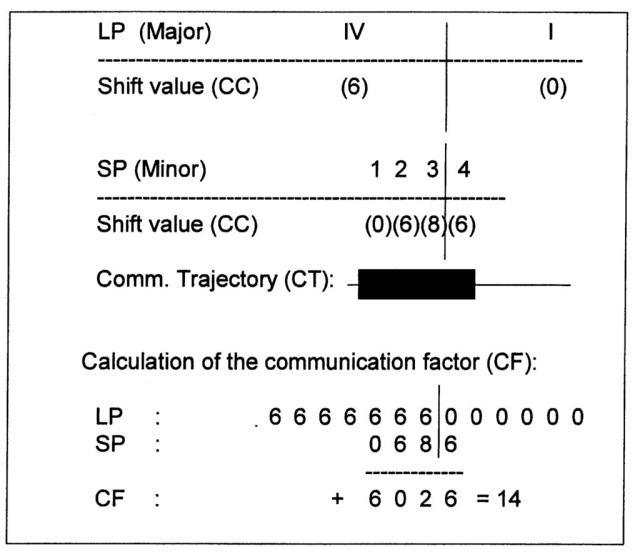
The new unit is called the communication factor (CF). The calculation of the given example (SP in the Fourth Quadrant of LP) is visualized in fig. 832.

Fig. 832 – A calculation of the sum of the communication coefficients (CC) over the communication trajectory (CT). The Small Part (SP) is fully embedded in the Fourth Quadrant of the Large Part (LP). The new unit of measurement is called the Communication Factor (CF).

The communicationfactor (CF) can be defined as follows:

The communication factor (CF) is the sum of the differences between the communication-coefficients (CC’s), calculated over the communication trajectory (CT).

The communication factor (CF) is the most important unit of measurement in the quadralectic philosophy. It defines the shift (as a degree of commensurability) between the communication partners over a given trajectory.  It is not a particular point, but gives a range. The CF-value is an indication for the state of affairs in a communication over a certain trajectory and can be related to forms of visibility. A (numerical) figure acts as in indicator for a distance between communication partners. This figure (of the CF) is determined by the length of the Small Part (Minor).

The next phase in the shift of the Small Part (or Minor) along the Large Part (LP) – still to the right – involves an ‘intrusion’ of the Fourth Quadrant of the Minor into the First Quadrant of the Major. This new situation cannot be measured at first, but the circumstance change when the boundaries of a compartment of the Minor coincide with those of the Major.

The different options – in movements and directions between the parts – will be looked in due course, but the present example is just a way to indicate the procedure.

It can be imagined, that the Small Part (SP) passes along the First Quadrant of the Major (LP) and that the boundary between the Third and Fourth Quadrant (of SP) coincides with the boundary of the Fourth and First Quadrant (of LP) if the movement continues.

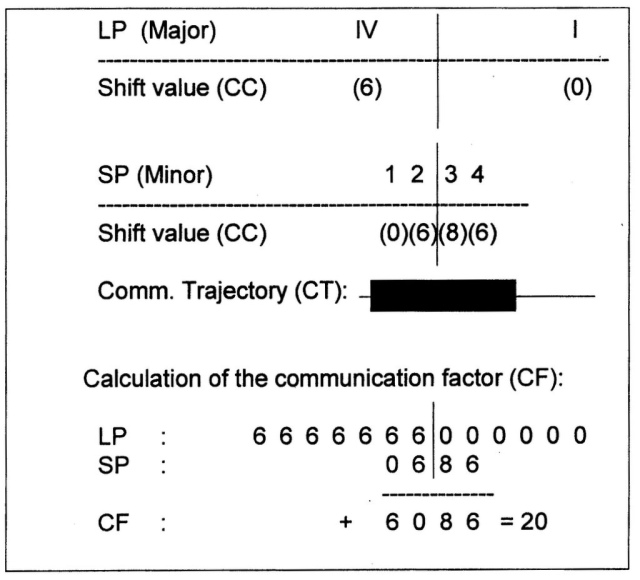
This situation is visualized in fig. 833. The communication factor (CF) in this particular situation is calculated in fig. 834.

Fig. 833 – A Small Part (SP) approaches a Large part (LP) from the left and the boundary of the third and fourth quadrant of the Minor (SP) coincides with the beginning of the first quadrant of the Major (LP).

Fig. 834 – The calculation of the CF-value when a Small Part (SP) moves along a Large Part (LP) from left to right.

Again a phase of immeasurability occurs when the movement of the Minor (SP) continues along the Major (LP). This part of the trajectory could be called the ‘in between’ (like it is also known from the paradoxes of Zeno). There is an interaction between the communication partners, but there are no measurable points of reference on this given stretch of the journey. It is important to note that the actual size of this part of the itinerary has no influence on the calculations.

The following rule is of the utmost importance (on a philosophical level) in the establishment of a formalized interaction between communication partners in a division environment.

A measurement of the differences in communication coefficients (CC’s), generated in a linear shift movement between divisions, can only be made when boundaries (of subdivisions) coincide.

The shift between the (sub) divisions yields an alternation of specific points of measurements (in the case when boundaries coincide) and areas of immeasurability (when boundaries do not coincide).

The next point of measurability (in the previously given example of a SP passing along an LP to the right) takes place when the boundaries of the 2-3 quadrant (of the Minor) coincide with the beginning of I-quadrant of the Major. This position is represented in fig. 835:

Fig. 835 – A small four-division SP (1-4) shifts along a large four-division (LP) to the right. The boundary of the second and third quadrant (2-3) of the Minor (SP) corresponds in this example with the beginning of the Major (LP), i.e. the boundary between the fourth and first quadrant (IV-I). The actual size of the com-partments is not of influence on the calculations, which are made on a purely theoretical level.

The calculation of the communication factor (CF) in this particular situation is as follows (fig. 836):

Fig. 836 – An example of the calculation of the CF-value in a hypothetical linear shift- model between two four-divisions. The Small Part (SP) passes here, from left to right, along a Large Part (LP).

The boundary of the second and third quadrant of the SP (2–3) corresponds with the beginning of the first part of the LP (IV-I). The final CF-value is calculated over the communication trajectory (CT), which is determined by the size of the smallest part (SP).

The generation of measurable points continues during the course of the Minor (SP) along the quadrants of the Major (LP) in very much the same way.  Every time a point of measurement (when boundaries coincide) is followed by an ‘immeasurable’ trajectory when the boundaries of quadrants do not coincide. The ‘in between’-trajectory is characterized by the anticipation of an indefinite number of measurements. They are, notwith-standing, in relation to the fixed values derived from points of coincidence, just arbitrary quantifications. Their value is confined to the range given by two ‘fixed’ CF-values on both sides of the point of measurement.

After the First Quadrant (I) of the Major (LP) has been passed by the Small Part, it will continue its route along the Second (II), Third (III) and the Fourth Quadrant (IV). In the end, all the quadrants of SP (Minor) have moved along all the quadrants of LP (Major), and the communication trajectory will be completed.

The full shift-sequence is now given in fig. 837 and the CF-values are graphically represented in fig. 838:

Fig. 837 – The CF-values of a complete shift of a Small Part (SP) along a Large Part (LP), moving from left to right.

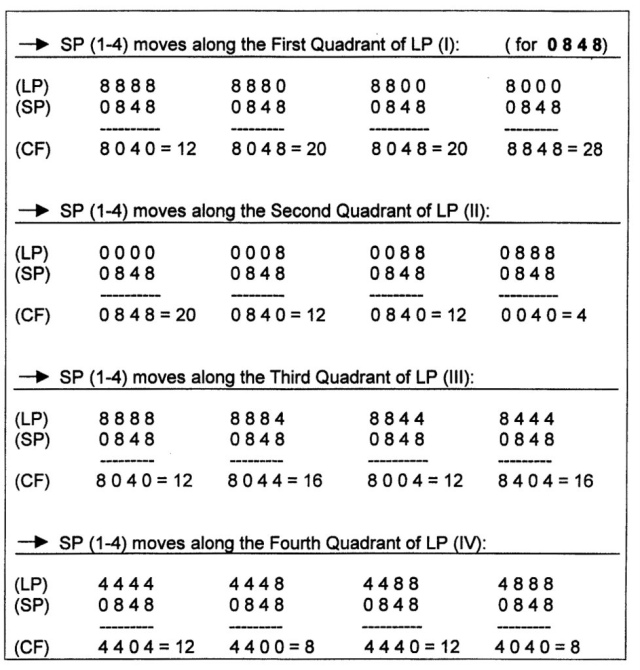
The shift result in the following CF-values (for the A-sequence 0 6 8 6):

8     14     20     26     20     14     8     2     8     10     8     10     12     10     12     10

This sequence of the measurable points indicates the relative ‘distances’ between any given LP and SP, which partake in a communication. High values of the communication factor CF – the maximum here is 26 – convey a greater distance between the division-partners or farness. Low CF-values – the minimum is 2 – point, on the other hand, to a diminished distance or increased proximity of the participants.

Fig. 838 – The thirty-two  (32) basic situations in a shift between two abstract four-divisions. The Major (LP) consists of the quadrant I – IV and the Minor (SP) comprises the quadrants 1-4. The displacement sequence 0 6 8 6 (A-series) is used here and the Minor (SP) moves from left to right. The number underneath the shift gives the communication factor (CF) at that particular situation.

The sixteen consecutive CF-values provide a numerical blueprint of a dynamic communication carried out by two unequal four-divisions in a cyclic environment. This CF-sequence can be defined as follows:

A CF-sequence is a collection of CF-values, which is generated when two communication partners perform a complete shift over the communication trajectory.

This process of shifting quadrants must be fully understood before we can continue to other possibilities and directions within a communication. The  creation of a value-system for a quadralectic communication hinges on the independence of the direction of approach. The measurements should be orientational ‘neutral’. The quadralectic valuation has a cyclic nature and eradicates all references to a particular direction within a shift.

Sofar, the shift procedure was based on a move from left to right and now a shift from the ‘opposite’ direction will be investigated. Fig. 839 gives the ‘start situation’ of a dynamic Small Part (SP, Minor) approaching a static Large Part (LP, Major) from right to left. The first compartment of the SP (1) makes contact with the last department of the LP (IV).

Fig. 839 – A dynamic SP (Small Part) moves from right to left along a static LP (Larger Part). The illustration shows the moment when the first quadrant of the SP (1) comes in contact with last quadrant of the LP (IV). The subsequent quadrants of the SP will cross the same boundary one after another and measurement will be possible if boundaries coincide.

The movement-to-the-left of the SP (Minor) along the various quadrants of the LP (Major) continues in the same way as a movement-to-the-right. Measurements are only possible when boundaries of (sub)division coincided. The intermediate area cannot be measured directly. The size of the ‘in between’ area is not important for the calculations.

An overview of CF-values is given in fig. 840 when a SP (Minor) moves from right to left along a LP (Major). The calculated CF-values represent the situation when boundaries coincide:

Fig. 840 – The complete shift of a Small Part (SP) along a Large Part (LP), moving from right to left,  for the A-sequence 0 6 8 6.

The following sequence is the result of that movement:

20     26     20     14     8     10     12     10     12     10     8     10     8     2     8     14     

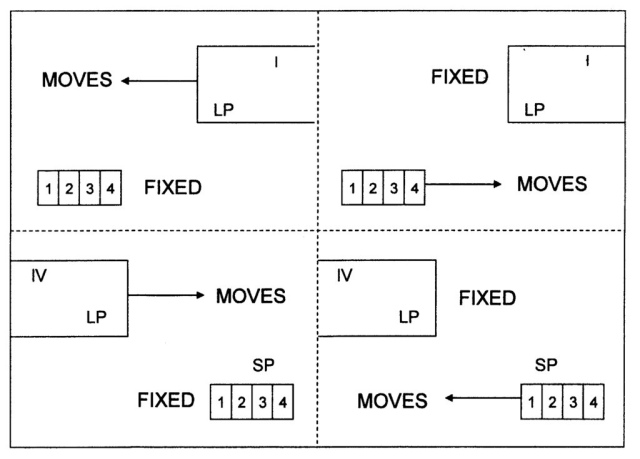
The previous examples showed a dynamic SP (Minor) which moved along a stable LP (Major), either from left to right (4 touches I; fig. 837) or from right to left (1 touches IV; fig. 840). A reverse situation is also possible, when the SP (Minor) is stable and the LP (Major) is dynamic. This circumstance produces two shifts. An overview of the theoretical possibilities is given in fig. 841:

Fig. 841 – An overview of the four possibilities of movement in the inter-action between a Large Part (LP) and a Small Part (SP). To the left: a dynamic Major moves in two directions (left – right) along a stable Minor. To the right: a dynamic Minor moving in two directions (right – left) along a stable Major.

Four CF-sequences are produced in this way (fig. 842):

Fig. 842 – The four possibilities of shift between two four-divisions.

There are always two sequences the same, in other words: the sequence of ‘LP-to-the-right’ is equal to ‘SP-to-the-left’ and the sequence ‘LP-to-the-left’ is equal to ‘SP-to-the-right’.

The CF-sequences can now be seen together, referring to the earlier shift results of the investigation (fig. 837 and fig. 840) :

The averages of the four ‘directions’ (: 4) gives a standard-CF-sequence which is independent of the direction of approach:

14     20     20     20     14     12     10     6     10     10     8     10     10      6     10      12

This sequence of CF-values is called the First Standard Sequence (FSS).  The series gives an indication of the distance between partners in a four division, calculated over the communication trajectory (limited by the Smallest Part). The interchange is valued by the most common CC-sequence (0 6 8 6) and is independent of the direction in which the divisional parts move along each other.

The formulation of the First Standard Sequence (FSS) is not the end of the procedure, because all the possibilities are not exhausted. This particular sequence was generated from the CC-sequence 0 6 8 6 (or A-series).

Fig. 829, at the beginning of this chapter, showed sixteen combinations (of the classic sequence 1 2 3 4) with such shift series. However, there were also eight displacement series with a CC-sequence 0 8 4 8 (the so-called B-sequence).

The B-sequence has to be included in the communication to achieve a ‘universal’ parity. The whole procedure of a shift between a Minor and a Major, from left to right and right to left, has to be repeated, but now for the B-sequence. The consequences of the different number of combinations in the A-series (16) and the B-series (8) will be faced at a later stage. For now the main movement will be repeated in a somewhat abbreviated form.

The movement of the Minor along the Major (two possibilities) and the opposite movement of the Major along the Minor (two possibilities) will now be followed for the CC-sequence 0 8 4 8 (B-series). First with a movement from left to right (fig. 843/844), then with a movement from right to left (fig. 845). The sequences will be combined at the end to give the Second Standard Sequence (SSS).

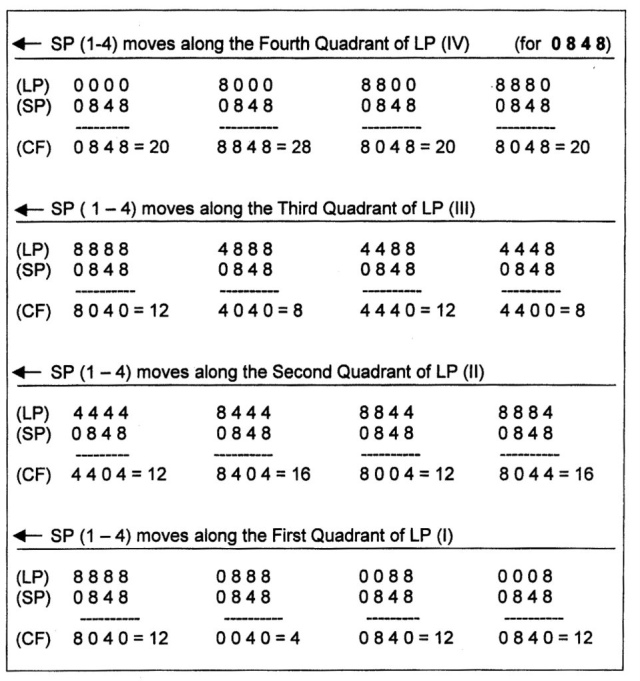
Fig. 843 – The complete shift of a Small Part (SP) along a Large Part (LP) moving from left to right, giving the following CF-values  (for the B-sequence 0 8 4 8):

12     20     20     28     20      12      12      4      12      16     12     16     12      8      12      8

The sequence of measurable points indicates – just like it did in the shift based on the 0 6 8 6 sequence – the relative distances between the Small Part (SP) and the Large Part (LP). The highest value (or greatest distance between the communication partners; also called remissio) is now 28, and is reached in the fourth position from the left. The lowest CF-value is 4 (greatest proximity of the communication partners; or intensio), is attained in the eighth position from the left.

The graphic expression of the full cyclic shift is illustrated as follows (fig. 844):

Fig. 844 – Thirty-two  (32) basic situations in the shift between two abstract four-divisions, using the B-sequence 0 8 4 8 as a calculation unit. The SP (Minor), consisting of the quadrants 1 – 4, moves from left to right along a LP (Major) comprising the quadrants I – IV. The number under the shift gives the communication factor (CF), which can be calculated in that particular situation.

The next consideration will be an approach ‘from the right’. This means that the SP (Minor) moves along the LP (Major) from right to left. The first quadrant of the SP enters, as a consequence, from the huge space of the first quadrant (of a following cycle) into the last quadrant of the LP (Large Part). Subsequently, the Minor passes along all the other quadrants of the Major in a reverse order. This movement is given in fig. 845.

Fig. 845 – The complete shift of a Small Part (SP) along a Large Part (LP) moving from right to left, gives the following CF-values (for the B-sequence 0 8 4 8):

20     28     20     20     12      8      12      8      12      16      12      16     12     4     12     12      

A summary of the various CF-sequences (of the B-sequence 0 8 4 8) will be given here:

Small Part moving to the right  (or Large Part moving to the left):

12      20     20     28     20     12     12     4      12      16      12      16     12     8     12      8

Small Part moving to the left (or Large Part moving to the right):

20     28     20     20     12       8     12      8      12      16      12      16     12     4     12     12

The standard row is derived from the mean of the four sum-series.  The calculation of the standard CF-series (with the 0 8 4 8-row as reference) is as follows:

The average of the four ‘directions’ (: 4) gives a standard CF-sequence which is independent of the direction of approach:

16      24     20     24      16     10     12      6     12      16      12      16      12    6     12     10

This sequence of CF-values, based on the displacement series 0 8 4 8, is called the Second Standard Sequence (SSS). The sixteen numbers are derived from a second path of thinking with a different displacement series (the B-series) as a point of departure.

Again, the row of consecutive CF-values gives an indication of the distance between partners in a four division, calculated over the communication trajectory (which is limited by the Smallest Part). The interchange is now valued by  the CC-sequence (0 8 4 8) and is independent of the direction in which the divisional parts move along each other.

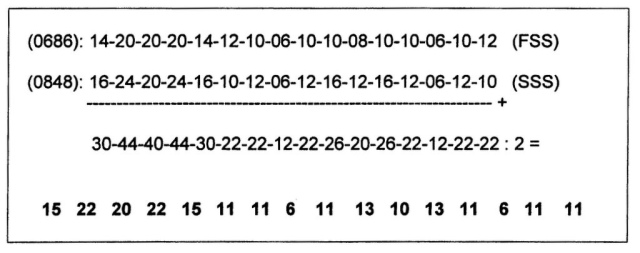
The final calculation is now to join the two standard-CF-sequences (FSS and SSS), i.e. the one derived from the A-sequence 0 6 8 6 and the other acquired from the B-sequence 0 8 4 8 and take their average value.

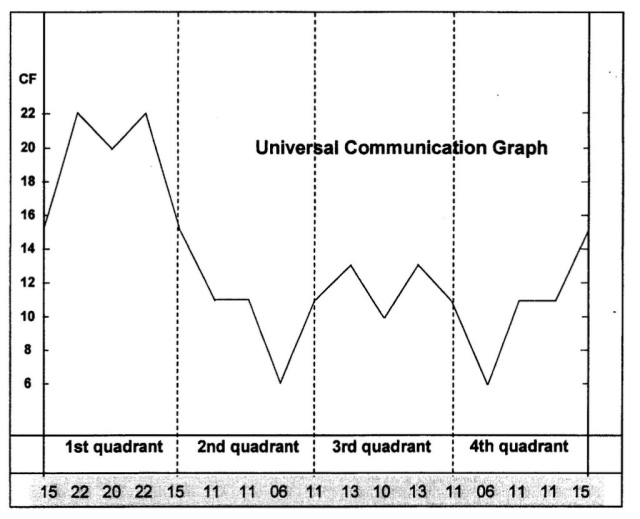
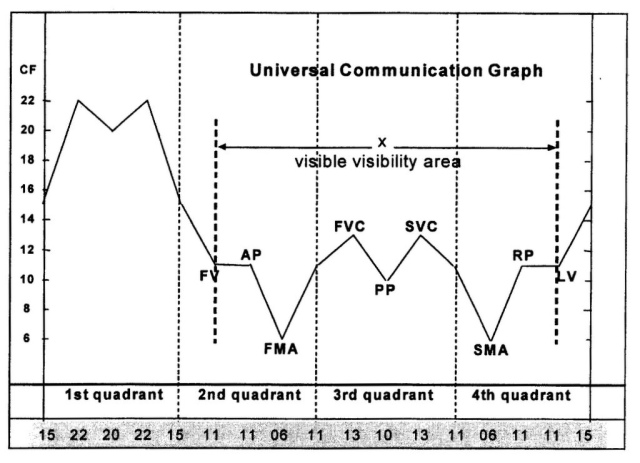
This CF-sequence is called the universal communication sequence (UCS) and can be expressed as a universal communication graph (fig. 846). This sequence (or CF-graph) is by far the most important expression of the quadralectic way of thinking. It indicates the measure of commensurability in terms of intensio and remissio for any given communication based on a four-division.

Fig. 846 – The UNIVERSAL COMMUNICATION SEQUENCE (UCS) drawn as a graph from the CF sequence: 15  22  20  22  15  11  11  06  11   13  10  13  11  06  11  11  15

The graph of the UCS is a universal representation of the receding and approaching actions, which takes place between communication partners in any conceivable interchange based on a four division. Every observation has its given place within the interaction and can be understood from that particular location.

An important point must be considered before the universal representation can be put into practice. The primary fragmentation offered twenty-four possibilities to arrange a four-partition (fig. 826). Sixteen types resulted, after an internal shift, the A-sequence (0 6 8 6) and eight produced, after an internal shift, the B-sequence (0 8 4 8) (fig. 827).

The question can now be raised if these differences in number should be taken into account when the final average is calculated. In other words: to count the sixteen (16) possibilities of the A-sequence proportionally more than the eight (8) possibilities of the B-sequence, i.e. in the proportion of two to one. The fundamental choice between a weighted average (1: 2) and an equal contribution (1:1) to the outcome  confronts the observer with a renewed awareness of the position in the process.

The application of a weighted average (or pro-rata contribution) is a formal ‘Third Quadrant’ solution, with the emphasis on the number-as-part. The calculation of the average (of FSS and SSS) follows the rules of arithmetic and uses the ratio (2 : 1) in a consequent way. The use of the equal contribution is rendered as a ‘Fourth Quadrant’ solution, with the emphasis on the dynamic aspect of the number-as-multitude.

The choice between number-as-part (III) and number-as-multitude (IV) is not new. Lady Arithmetica is seen here to offer the choice between the two different approaches towards figures. To the right: Pythagoras with the abacus (system), based on a static-spatial setting of figures. To the left: Boethius, using the dynamic Arab figures, which are independent from a geometric source. First given in: RIESCH, G. (1583). Margarita Philosophica. Bazel. Also in: LAWLOR, Robert (1982). Sacred Geometry. Philosophy and Practice. Thames and Hudson, London.

The handling of the two types of calculations is a noticeable ‘weakness’ in the objectivity of the result (the UCS). The necessity to make a choice or subjective intervention is the only way to go beyond the constraints of oppositional thinking. The two primary results (FSS – SSS) are given a new space of interaction in the dynamic fourth subdivision (of the Second Quadrant). The choice (between the valuation of two types of sequences) creates an opening and leads eventually to a universal unity.

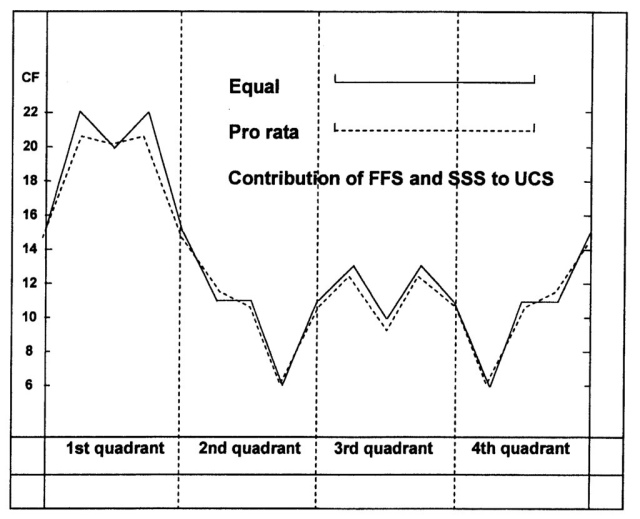
The difference between the results (fig. 847/848) lies in a somewhat lower remissio in the First and Third Quadrant (lower CF-values) in the pro-rata graph. Furthermore, the absence of the areas of equilibrium in the second division of the Second Quadrant and the third division in the Fourth Quadrant is noteworthy. The boundaries of the Third Quadrant are not fixed at the value of CF = 11, as in the case of the UCS, but they have a slightly lesser value. The points of maximum intensio are the same in both graphs (CF = 6).

Fig. 847 – The difference of the CF-graph as based on an equal contribution (1:1) of the two basic standard sequences (FSS and SSS) and a pro-rata (1: 2) contribution of these sequences to the result of the Universal Communication Sequence (UCS). The former possibility is given with a regular line and the second choice with an intermittent line.

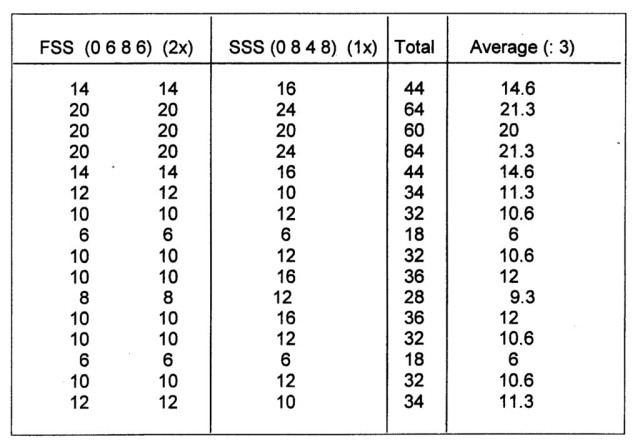
The shape and values of the two graphs do not, in general, differ a great deal (fig. 848). Therefore, the choice between the rounded figures – as a result of the equal distribution (1: 1) – in favor of the broken figures of the pro-rata distribution (1 : 2) is chiefly inspired by a practical attitude. The option of the equal distribution, as a ‘Fourth Quadrant’ solution with the emphasis on the multitude, has been chosen to form the final CF-sequence.

Fig. 848 – The calculations of the weighted averages of the pro-rata distribution of the two CF-sequences (2 x FSS and 1 x SSS), which contribute to the outcome  of the Universal Communication Graph (UCG).

It must, once again, be understood that this choice is part of a subjective intervention, which  could form – from a rigid (old-fashioned) scientific point of view –  an obstacle to accept the quadralectic way of thinking. By doing so, it will – unfortunately – also reject the use of the CF-graph as a mighty tool to support the meaning of visibility.

It is worthwhile to pause at this point of the inquiry to recapitulate once again the imaginary track, which has been followed so far (fig. 849). Every step must be meticulously charted now the first general picture emerges. Quadralectic thinking is logical in its own way.

Fig. 849 – This diagrammatic scheme illustrates the intellectual journey (‘Tao of quadralectics‘) into a comprehensive communication based on a four-fold division.

The whole primary operation of division and shift is situated in the Second Quadrant, but the characteristics of the Third and Fourth Quadrant made their presence clear in advance (in the subdivision). Therefore, a wider setting of the various cognitive actions must be understood in this early stage. The procedure in the Second Quadrant is an anticipation of the things to come. The cyclic setting means that all things are already there, as pack and parcel of visibility-as-a-whole.

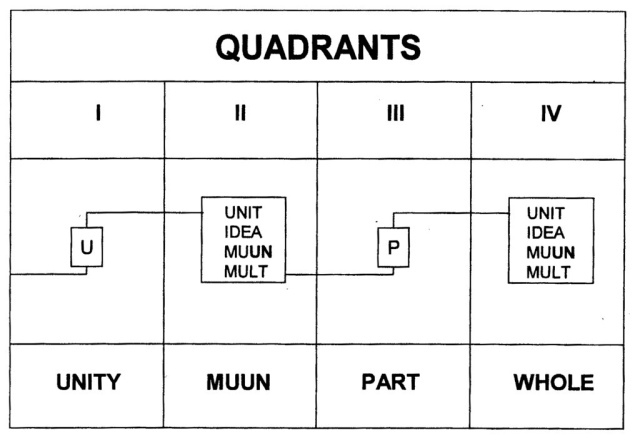
The relationship consists of a unity U (in the First Quadrant), which is fragmented by a four division in the Second Quadrant. The integral communication is enacted in this quadrant. The unity gives rise (after division) to an idea (of movement). The resulting interaction (of subdivisions) can be validated as a muun (multi-unity). This ‘virtual’ entity can act as a new standard (of measurement) in a (visible) multitude. An area of subjective intervention (UN; dark outlined) is essential in the continuation of the interaction.

The path through the subsequent stages of interaction between the four divisions of a communication is a reflection of the way of thinking itself. The actual procedure consists of four major stages in which human thoughts can dwell. Firstly, they can be located in the unity of the undivided (static) presence, without any visibility (I). Secondly, they concern themselves with the division/fragmentation into units (a muun) and – simultaneously – experiences a shift of those (sub) divisions. Visibility (in the form of repeated recognition) is gained in this process (II). The third (static) step is the creation of a unit of measurements (a part), derived from the chosen division. An actual empirical presence or visible visibility can be achieved at this stage (III). The fourth and final move is the implementation of the unit (of measurement/the part) in a dynamic interchange with other units (parts), leading to a new understanding of the whole (IV).

This procedure is, in a nutshell, the four-fold way of thinking. It brings about the quadralectic vision in a logic sequence of actions and ends in a tool (the CF-graph) to tackle every possible communication. However, one important item remains to be solved before the CF-graph can function in the world of lower division thinking. Where is the boundary of the visible and invisible world? What is the definition of visible visibility and where does it start?

The CF-graph provides a unique guide in the complexity of reality. Because now it becomes clear, that ‘visibility’ in a dualistic environment is completely different from visibility in a tetradic territory. In the first case, a dual frame of reference is used, which means that differences in a relation are reduced to their oppositions.  In the second case, in a wider field, there are also differences, but now the aim is a search for similarities and resemblance and the active role of the observer in this search is acknowledged.

If the quadralectic mood will be understood by the dialectic frame of mind, it is necessary to widen the scope of the latter and lift the restrictions of visibility.  The nature of duality prescribes a widening in the ‘visible area’, because there is no gradation in the invisible area. When a quadralectic mind talks of invisible visibility than the dualistic frame of reference got confused.  Only in the Third Quadrant (of the quadralectic division), which is governed by visible visibility and a unit of measurement, a concordance of quadralectic and dialectic thinking is easier to understand (for the latter frame of mind).

The part P, as a visible proof of division, is the vital link between the lower and higher stages of division thinking. The highest understanding is found in the pinnacle of lower division imagination, i.e. the material, when the Third Quadrant opens with the CF-value of 11.

The definition of visibility is part and parcel of the third step in the Second Quadrant, even before the actual visibility of the Third Quadrant has shown itself. The creation and notion of (visible) visibility is a monumental event and the crown on the inquiry into the nature of communication. The CF-graph, as the product of a creative exercise (of shifting four- divisions), holds the key to a genuine representation of the interchange between the communication partners.

The rigid approach to visibility, in a dualistic environment, demands an exact figure (of the CF-value) in order to participate in the understanding of the CF-graph from its own (limited) point of view. A subjective interpretation of the graph-as-a-whole is required in order to bridge the gap of comprehension. This necessity has led to the proposal to put the boundary of empirical visibility at the value of CF = 11.

The arguments for this choice are, first and for all, the noticeable beginning (and end) of the Third Quadrant (III) with this particular CF-value. The Third Quadrant embodies the (visible) part P in the quadralectic view, although  CF-values within the quadrant vary considerably. Two ‘highs’ (CF = 13) and one ‘low’ (CF = 10) are characteristic of the Third Quadrant. A quadralectic mind perceives this setting of subdivisions as a repetition of the major four-partition on a smaller scale. The dualistic mind only sees a part or not a part, without any intermediate stages.

The second consideration to put the (visible) visibility boundary at CF = 11 is provided by the distinct horizontal lines in the second part of the Second (II, 2) and the third part of the Fourth Quadrant (IV, 3).  The CF-graph reached some sort of equilibrium at the value of CF = 11 at those particular moments/places in the progress of a universal interchange. They represent the only events on the CF-graph where the continuation is not associated with a change in intensio (approach) or remissio (alienation). This typical capacity provides a boundary in its own right.

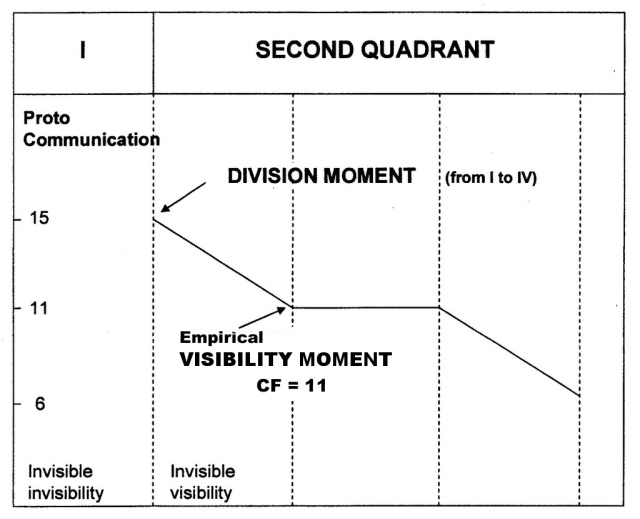
The start of the visible visibility in the Second Quadrant (at the CF-value of 11) is visualized in fig. 850.

Fig. 850 – An overview of the various important moments at the start of a four-fold communication. The primary choice towards a four-fold interaction takes place at the beginning of the Second Quadrant (II, 1).  The beginning of the empirical visibility on the CF-graph starts at the beginning of the second quarter of the Second Quadrant (II, 2). The CF-values reach the value 11 for the first time. This identification implies that every communication, which makes itself known and has a certain extension, is preceded by an invisible period (of 5/16 V), called the proto-communication.

The choice of the CF-value 11 as the beginning of empirical visibility makes this value of special importance within a quadralectic setting.  The correct interpretation is the very moment where the dialectic and quadralectic thinking diverges. The oppositional thinker envisages only two possibilities:

1. The absolute way is keeping to the letter of the definition. This means: under CF = 11 visible, over CF = 11 invisible. This mental position has to be placed in a Third Quadrant environment. If we apply this strict rule to the Third Quadrant-as-a-whole, it turns out that the visibility (of the Part) is not very prominent. In other words, the part does not have a good view of itself, in terms of its own definition. Most CF-values in the Third Quadrant are higher than the (arbitrary) ‘visibility-boundary’ CF = 11 and only the area around the CF-value of 10 qualifies for a ‘real’ visibility in an empirical sense. The greater visibility in terms of intensio are reached in the Second and Fourth Quadrant, when the CF-values reach their lowest points (CF = 6).
2. The multiple way anticipates the dynamic visibility of the higher division thinking. The intellectual position dwells in a Fourth Quadrant environment. Polarity, as an oppositional rigidity, is left behind and a quadralectic setting of the CF = 11 value gets a new meaning. Polarity is replaced by plurality. The conscious use of four types of visibility – in every stage of the communication – puts the empirical visibility in its proper place. It is just a static moment in time, with limited boundaries, in a sequence of other observances. The multiple way opens a gateway to the width of the Fourth Quadrant, with a recapitulation (and understanding) of a full communication.

Fig. 851 gives a comparison between the ‘absolute’ (CF<11) visibility in a dualistic and quadralectic approach.

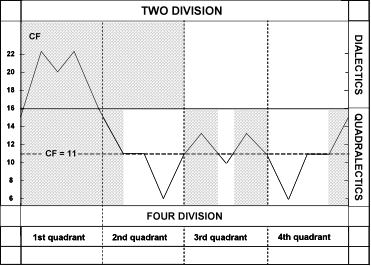Fig. 851 – A graphic expression shows the comparison between the areas of empirical visibility in a dualistic and quadralectic environment. The CF-value 11 is used here in an absolute sense to indicate the boundary of (visible) visibility. The upper box with the dualistic vision has the dividing line between the visible and invisible right in the middle of the total communication. The lower box shows four areas of invisibility (dark) and three of visibility (light), representing the quadralectic perception.

The definition of visibility in the form of a single CF-value is the ultimate treasure and crown of a voyage, which had no beginning and no end. Visible visibility (including our own presence in this world) is the result of a special interaction between communication partners, in which the choice of a (primary) division is of the utmost importance. Here we are, as the observer, standing in a universe of unimaginable dimensions and only equipped with our own ability to order the observations in a comprehensive way. CF = 11 looks like the Philosophers Stone in an alchemists’ dream.

A nomenclature was given to the Universal Communication Graph (UCG). It gives the major moments in the communication cycle (fig. 852). In particular, the inflection points in the visible visibility area (X) have been given names to facilitate the description of the character of these particular positions. The area X is defined as that part of the CF-graph – running from the first occurrence of the CF-value 11 in the Second Quadrant to the last occurrence in the Fourth Quadrant – in which empirical study is possible. Outside this area (in the First Quadrant, the first part of the Second Quadrant and in last part of the Fourth Quadrant) such a study is not possible  and belongs to the realm of belief and metaphysics.

Fig 852 – The CF-graph with the visible visibility area X and the various deflection points, which are described in the text.

The visible area  (X) of the CF-graph contains the following punctuations, or deflection points of the line:

———————————–  FV      –  First Visibility

———————————–  AP      –  Approach Point

———————————–  FMA  – First Major Approach

——————-  The boundary between Second and Third Quadrant (II – III) ————–

————————————  FVC   – First Visibility Crisis

————————————  PP      –  Pivotal Point

————————————  SVC   –  Second Visibility Crisis

——————-  The boundary between the Third and Fourth Quadrant (III – IV) ———

————————————  SMA   – Second Major Approach

————————————  RP     –  Receding Point

————————————  LV    –    Last Visibility

The vertical axis of the graph shows the values of the communication factor  (CF).  The communication factor CF is a measure for the maximal  (CF = 22) or minimal shift (CF = 6) between the partners, which participate in a communication based on the four-division. The concepts of ‘approach’ (intensio/attraction) and ‘alienation’ (remissio/estrangement) provide, in turn, a possibility to describe and evaluate the communication. It must be understood that the above-given polarity finds its origin in the oppositional way of thinking. Quadralectic thinking does not put a value on one of these processes, but values the process-as-a-whole. The marker points in the visibility area X will now briefly be described:

FV –   The First Visibility is defined as a distinction in time and place of the first (measurable) recognition between the communication partners. The event takes place at the beginning of the second subdivision of the Second Quadrant (II, 2), when the critical value of CF = 11 is reached. The FV is located at 5/16th part of the full communication cycle V.

AP –   The Approach Point marks the position on the CF-graph where the CF-values drop for the first time below the value of CF = 11. This point lies at the end of the second subdivision of the Second Quadrant (II, 2). The AP is fixed at 3/8th part of the quadralectic cycle V and at 1/10th part of the visible visibility area (X).

FMA – The First Major Approach is characterized by the lowest CF-value on the CF-graph (CF = 6) at the end of the third subdivision in the Second Quadrant (II, 3). The FMA has the greatest intensio, which means that the maximum approach in the communication will be gained at this point.

FVC – The First Visibility Crisis is situated at the end of the first subdivision in the Third Quadrant (III, 1) where the CF-value (CF = 13) reaches for the first times its greatest remissio (or alienation). This process causes tension within the communication and can result in mental confusion or some sort of ‘identity crisis’.

PP  –   The Pivotal Point is situated in the middle of the visible visibility area X and also in the middle of the Third Quadrant, and the end of the second part (III, 2). The point lies on a vertical symmetry axis, which mirrors the values of the CF-graph (restricted to the area X). The oppositional character is consciously felt since the CF-value is 10, i.e. within the realm of visible visibility.

SVC – The Second Visibility Crisis is to be found at the end of the third subdivision in the Third Quadrant (III, 3) where the CF-value (CF = 13) reaches for the second times its greatest remissio (or alienation). Again the tension mounts as a result of the alienation, but now with regards to the material side (in terms of gains and loss).

SMA – The Second Major Approach is identifiable by the lowest CF-value on the CF-graph (CF = 6) and is situated the end of the first subdivision in the Fourth Quadrant (IV, 1). The SMA has – just like its predecessor the FMA – the greatest intensio, resulting in a maximum visibility of the essential elements of the communication. All potential possibilities (of the FMA) are now materialized and can be appraised.

RP  –   The Receding Point marks the start of a period of equilibrium (CF = 11) at the beginning of the third subdivision of the Fourth Quadrant (IV, 3)  The RP is fixed at 7/8th part of the quadralectic communication cycle V and at  9/10th of the visibility area X.

LV   –  The Last Visibility is the antagonist of the First Visibility (FV) and situated at the very end of the visibility area X, where the CF-value 11 is reached for the last time. The location is at the end of the third part of the Fourth Quadrant (IV, 3). It signifies the last notion of (measurable) recognition between the communication partners. The LV is located at 15/16th part of the full communication cycle V.

These inflection-points (on the universal communication graph, UCG) can be seen as points of recognition (POR). Any conceivable communication – based on a four division – will go through the same pace. The recognition is a moment of connection between the observer (signifier) and a particular situation (signified). It provides a distance in a communication, expressed in visibility.

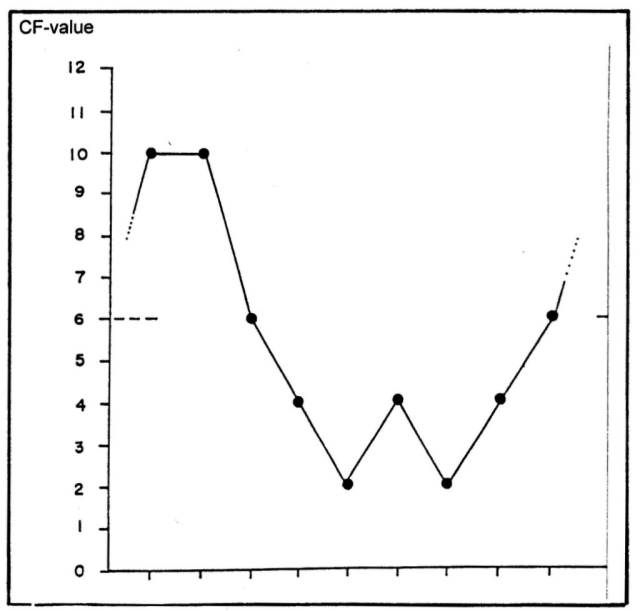
Quadralectic (four-fold) thinking is an evolutionary development within the psychological history of mankind. It started with the two-division as a survival strategy. The next step is the three-division, which offers room to intermediate positions. The theoretical base of the three-division was earlier studied by the writer (1992/1997) and resulted in a simple CF-graph (fig. 853). The three-division has only one set of shift-values (0 4 4).

Fig. 853 – The CF-graph of a theoretical three-division was created in the same way as the four-division by shifting two three-divisions along each other.

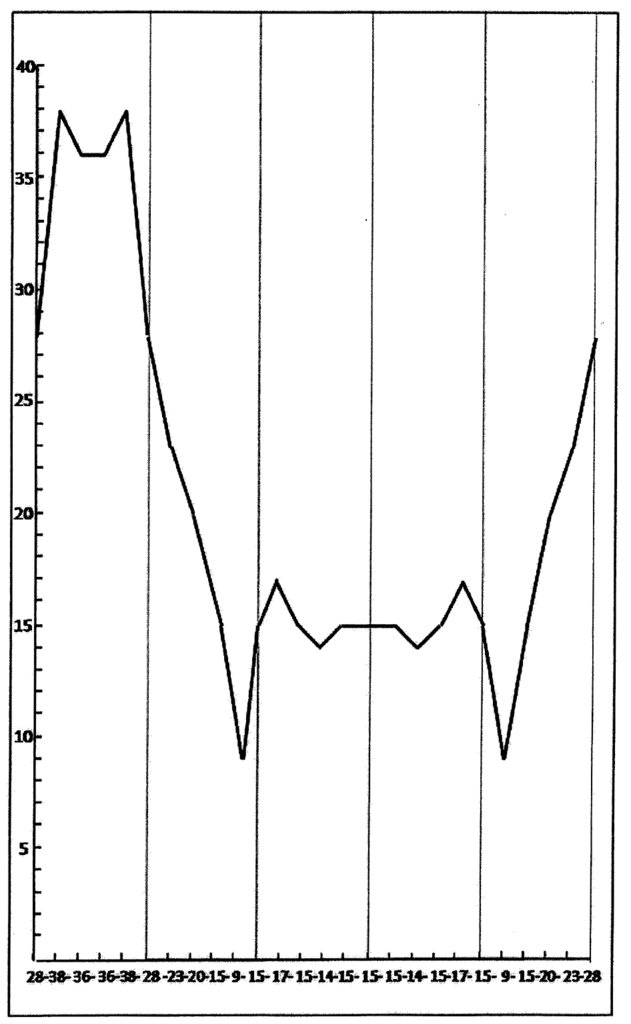
The ‘Chinese’ or five-division offers a further insight into the world of higher division thinking. The theoretical possibilities came to the foreground (in April 2008) when the relation between the Eastern and Western cultures was seen as an encounter of different ways of (division) thinking.

Fig. 854 – The universal CF-graph of a communication based on the five division. The generation was a process of a shift between two five-divisions, eliminating the directions and take the average of the various rows of shift values (A – C).

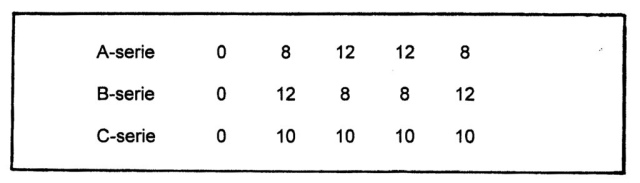
The study of the (universal) communication based on the five-division resulted in a CF-graph (fig. 854). The procedure was the same as followed in the four-division. The sequence 1 2 3 4 5 gave 120 types of different ordering sequences. A comparison with the other sequences gave only three different types of displacement series (A – C) in the five division. The distribution of these series was equal in the 120 types of sequences.

The four division gave two displacement series A (0 8 4 0) and displacement series B (0 8 4 8) and the three-division only one (0 4 4). Further mathematical study will (probably) reveal that:

The number of displacement series in a sequence of n-numbers is always (n – 2).

An evaluation of the division sequences (1-2-3) (1-2-3-4) and (1-2-3-4-5) points to a further specification of a general trend in every communication:

———————-        an alienation

———————-         a movement towards a (first) approach

———————-         a pivotal point

———————-         a movement towards a (second) approach

———————-         an alienation

This type of movement in a communication is positioned in a circular setting, which means that the alienation of stage 1 is, in fact, the same as the  alienation (remissio) of stage 5. Therefore, any communication – regardless of the initial number of division elements – goes through the following stages:

alienation         –         approach          –         pivotal point          –           approach

The four stages – as given here in their most general description – fit in perfectly in a general characterization of a quadralectic communication. Observations find their roots in the immeasurable space and time of the universe (First Quadrant). They become our own observations when the distance between the observed and the observer comes within reach of our own understanding (Second Quadrant). This understanding  follows after a division takes place. The pivotal point – with a devotion to symmetry –  epitomizes that very moment (Third Quadrant). A new intensio takes place once the nature of that primary division is understood (Fourth Quadrant).

This short expose of the quadralectic philosophy leaves a number of questions open, but no further elaboration will take place at this stage. The present book deals with quadralectic architecture, which means that the emphasis is primarily on the latter subject. Quadralectic thinking, although a philosophy in its own right, will be a means to reach an end – which is to describe architecture from a different point of view. However, without any knowledge or understanding of the modern four-fold way of thinking, the whole exercise becomes futile.

The discrepancy between the visible and the interpretation of the visible has too often been disguised, misunderstood or plainly ignored.